num_vector <- c(1, 4, NA, NaN)
num_vector[1] 1 4 NA NaNis.na(num_vector)[1] FALSE FALSE TRUE TRUE19 Fehlende Werte
Es kann in der Praxis häufiger vorkommen, dass Datensätze unvollständig sind z.B. wenn Teilnehmende einer Befragung nicht alle Fragen beantworten. Diese fehlenden Einträge nennt man Missings. In R werden sie (bei numeric) zumeist mit NA (not available) gekennzeichnet.
Welche Kodierungen für fehlende Werte gibt es neben NA noch?
Beim Datentyp numeric (Zahlen) sind fehlende Werte durch NA oder durch NaN (Not a Number) gekennzeichnet.
Die Funktion is.na() gibt für jedes Element ein TRUE wenn es fehlt bzw. ein FALSE wenn es vorhanden ist. Wir werden im Laufe des Kapitels verschiedene Kombinationsmöglichkeiten für diese Funktion kennen lernen.
NaN entstehen z.B. bei unlösbaren Rechnungen wie Division durch \(0\).
num_vector[1] <- num_vector[4]/0
num_vector[1] NaN 4 NA NaNis.na(num_vector)[1] TRUE FALSE TRUE TRUEBeim Datentyp character (Buchstaben, Zeichen) hingegen könnten fehlende Eingaben auch durch "" (leere Felder) gekennzeichnet sein z.B. wenn bei Freitextfeldern in einer Umfrage nichts eingegeben wurde. Das wird in R aber nicht automatisch als fehlender Wert erkannt.
Achtung: Wir sehen nachfolgend auch verdeutlicht, dass
NAeine selbstständige Kodierung ist, und nicht als character kodiert wird.
char_vec <- c(NA, "NA", "")
char_vec[1] NA "NA" "" is.na(char_vec)[1] TRUE FALSE FALSESpäter lernen wir, wie wir Werte auf NA umkodieren können.
NA in numerischen Datentypen (d.h. quantitative Daten).
Fehlende Werte sind grundsätzlich mit drei Schwierigkeiten verbunden:
- Der Datenausfall führt zu einer reduzierten Stichprobengröße \(N\) welche wiederum zu einer verringerten Effizienz bei der Parameterschätzung und geringerer Power führt.
- Die Auswertung wird erschwert, weil viele statistische Verfahren vollständige Datensätze voraussetzen.
- Wenn systematische Unterschiede zwischen den beobachteten und den fehlenden Daten bestehen könnten die Parameterschätzungen verzerrt sein.
Daher ist es sehr wichtig, sich vor der Auswertung einen Überblick über die fehlenden Werte zu verschaffen.
In diesem Kapitel schauen wir uns an, ob und wenn ja wo und wie viele Missings sich im Datensatz befinden. Außerdem gibt es einen groben Überblick darüber, ob Missings zufällig sind und wie man mit ihnen umgehen kann.
Der Umgang mit Missings ist ein komplexes Thema. In diesem Kapitel werden wir uns auf zwei gängige Methoden zum Umgang mit Missings beschränken. In Abhängigkeit der eigenen Fragestellung empfiehlt es sich, passende Methoden zu recherchieren.
Beispieldatensatz für dieses Kapitel
Das ist der Code für den Datensatz, an dem wir in diesem Kapitel arbeiten werden. Wenn du die Funktionen, die in diesem Kapitel vorgestellt werden, ausprobieren möchtest, führe den Code aus und erstelle den Datensatz.
# Data Frame erstellen
daten <- matrix(c(-99, 0, 1, 3, 2,
1, 2, 3, 2, 0,
NA, 1, 3, 99, 0,
1, 3, 3, 1, 2,
2, 0, 2, 99, 3), nrow = 5, ncol = 5)
# in Dataframe umwandeln
daten <- data.frame(daten)
# Spalten und Zeilen benennen
colnames(daten) <- c("Var_1", "Var_2", "Var_3", "Var_4", "Var_5")
rownames(daten) <- c("Vpn_1", "Vpn_2", "Vpn_3", "Vpn_4", "Vpn_5") Var_1 Var_2 Var_3 Var_4 Var_5
Vpn_1 -99 1 NA 1 2
Vpn_2 0 2 1 3 0
Vpn_3 1 3 3 3 2
Vpn_4 3 2 99 1 99
Vpn_5 2 0 0 2 3Achtung: Wenn du Variablen, die Missings enthalten, für eine Analyse nutzt, denke immer daran, dass sich damit auch die Stichprobengröße \(N\) für diese spezifische Auswertung ändert.
19.1 Sind die Missings einheitlich kodiert?
In manchen Anwendungen werden Missings nicht mit NA sondern anderweitig kodiert (z.B. bei Unipark mit 99 oder -99). Daher müssen wir dafür sorgen, dass R Missings auch als solche erkennt. Das gewährleistet man, indem man alle Missings auf NA setzt.
Wenn man weiß, wie Missings im Datensatz kodiert sind, kann man gleich zu Wie kann ich die Missings auf NA setzen? springen. Wenn man weiß, dass alle Missings einheitlich mit NA kodiert sind, kann man den ganzen Abschnitt auslassen.
19.1.1 Wie kann ich prüfen, ob die Missings einheitlich kodiert sind?
Um herauszufinden, ob auch alle Missings einer Variablen korrekterweise mit NA kodiert sind, vergleichen wir die angegebenen Werte der Variablen in unseren Daten mit den möglichen Ausprägungen der Variablen (die wir zumeist im Codebuch finden; in unserem Fall steht diese Information in der Einleitung).
Dazu kombinieren wir die Funktion unique(), die uns alle Werte eines Vektors (einmalig) ausgibt, mit der Funktion sort(), die uns die Werte noch sortiert (standarmäßig aufsteigend). Mit na.last = TRUE gibt uns sort() sogar die Information zum Vorhandensein von Missings am Ende aus.
sort(unique(daten$Var_3), na.last=TRUE)[1] 0 1 3 99 NADa wir wissen, dass Var_3 nur die Ausprägungen \(0,1,2,3\) annehmen kann, können wir schließen, dass \(99\) auch ein Missing sein muss.
Wenn man also alle möglichen Ausprägungen der Variablen kennt, kann man auf diese Weise einfach herausfinden, ob noch anderweitig kodierte Missings im Datensatz vorliegen.
Wenn der Datensatz sehr groß ist, ist der oben gezeigte Ansatz allerdings sehr mühsam. Dann können wir die Funktion sapply() integrieren, um unique() und sort() auf jede Variable im Datensatz anzuwenden. Diese hat die Form sapply(Daten, Funktion).
Da wir zwei Funktionen auf den Datensatz anwenden wollen - unique() und sort() - müssen wir sapply() zweimal anwenden:
sapply(sapply(daten, unique), sort, na.last=TRUE)$Var_1
[1] -99 0 1 2 3
$Var_2
[1] 0 1 2 3
$Var_3
[1] 0 1 3 99 NA
$Var_4
[1] 1 2 3
$Var_5
[1] 0 2 3 99In Var_1 gibt es die Ausprägung -99 und in Var_5 die Ausprägung 99, welche keine möglichen Ausprägungen sind. Es ist davon auszugehen, dass das ebenso Kodierungen für fehlende Werte sind.
19.1.2 Wie kann ich die Missings auf NA setzen?
Nun wollen wir diese Missings umkodieren. Vorher wollen wir uns noch einmal anschauen, was passiert, wenn man das nicht macht.
Wenn man Missings im Datensatz nicht einheitlich auf NA kodiert, nimmt R an, dass es sich um gültige Werte handelt. Das führt dann zu falschen Ergebnissen. Das schauen wir uns exemplarisch einmal am Mittelwert der Spalte Var_3 an.
Var_1 Var_2 Var_3 Var_4 Var_5
Vpn_1 -99 1 NA 1 2
Vpn_2 0 2 1 3 0
Vpn_3 1 3 3 3 2
Vpn_4 3 2 99 1 99
Vpn_5 2 0 0 2 3# Mittelwert vor Umkodierung
mean(daten$Var_3, na.rm=TRUE)[1] 25.75Nun kodieren wir die Missings in Var_3 einheitlich um …
# Umkodierung für einzelne Variablen
daten$Var_3[daten$Var_3 == 99] <- NADer Befehl ersetzt in daten Elemente der Spalte Var_3, welche die Ausprägung 99 besitzen, mit NA.
Var_1 Var_2 Var_3 Var_4 Var_5
Vpn_1 -99 1 NA 1 2
Vpn_2 0 2 1 3 0
Vpn_3 1 3 3 3 2
Vpn_4 3 2 NA 1 99
Vpn_5 2 0 0 2 3… und schauen uns den Mittelwert von Var_3 wieder an.
# Mittelwert nach Umkodierung
mean(daten$Var_3, na.rm=T)[1] 1.333333Hätten wir die Missings nicht einheitlich auf NA kodiert, hätten wir errechnet, dass der Mittelwert von Var_3 25.75 anstatt ~1.33 betragen würde.
Wir sehen also, dass es sehr wichtig ist, in Erfahrung zu bringen, ob im Datensatz alle Missings einheitlich auf NA gesetzt sind, und wenn nicht, diese einheitlich zu kodieren, da man sonst falsche Ergebnisse erhält.
Jetzt enthält die Spalte Var_3 schon keine Elemente mit der Ausprägung 99 mehr, aber in Var_1 gibt es noch ein -99 und in Var_5 noch ein 99.
Um nicht einzeln Spalten und Ausprägungen ansprechen zu müssen, kann man alles in einem Befehl kombinieren.
# Umkodierung für den gesamten Datensatz
daten[daten == 99 | daten == -99] <- NAHiermit werden im gesamten daten jene Elemente, welche die Ausprägung 99 oder -99 besitzen, durch NA ersetzt.
19.2 Enthält ein Datensatz Missings?
Wenn wir wissen wie unsere fehlenden Werte kodiert sind, wollen wir in einem nächsten Schritt natürlich wissen, ob ein Datensatz überhaupt Missings enthält. Es gibt zahlreiche Ansätze, um das herauszufinden. Einige davon schauen wir uns einmal genauer an.
Bei kleineren Datensätzen ist eine visuelle Inspektion möglich. Dafür nutzt man entweder View() (Großbuchstabe am Anfang beachten!) oder man klickt auf den Datensatz im Environment (oberes rechtes Panel).
Var_1 Var_2 Var_3 Var_4 Var_5
Vpn_1 NA 1 NA 1 2
Vpn_2 0 2 1 3 0
Vpn_3 1 3 3 3 2
Vpn_4 3 2 NA 1 NA
Vpn_5 2 0 0 2 3Um zu überprüfen, ob ein Datensatz mindestens einen fehlenden Wert enthält, kann man anyNA() nutzen. Man bekommt ein TRUE (d.h. ja, mindestens ein Missing enthalten) oder FALSE (d.h. nein, keine Missings enthalten) ausgegeben.
anyNA(daten)[1] TRUEUm einen groben Eindruck davon zu bekommen, welche Elemente fehlen, kann man is.na() nutzen. Der Output besteht aus FALSE oder TRUE für jedes Element des Datensatzes. TRUE bedeutet dabei, dass an dieser Stelle ein Missing ist.
is.na(daten) Var_1 Var_2 Var_3 Var_4 Var_5
Vpn_1 TRUE FALSE TRUE FALSE FALSE
Vpn_2 FALSE FALSE FALSE FALSE FALSE
Vpn_3 FALSE FALSE FALSE FALSE FALSE
Vpn_4 FALSE FALSE TRUE FALSE TRUE
Vpn_5 FALSE FALSE FALSE FALSE FALSEAchtung: Bei
is.na()undanyNA()wird auchNaN(Not a number; entsteht bei unlösbaren Rechnungen) mitgezählt. Da Zweitere aber wesentlich seltener vorkommen, konzentrieren wir uns nur aufNA.
Den logischen Vektor, den is.na() erzeugt, kann man mit which() kombinieren, um sich die Positionen der Missings ausgeben zu lassen. Mithilfe des Arguments arr.ind = TRUE lässt man sich die Reihe und die Spalte dieser ausgeben.
Ohne arr.ind = TRUE würde man nur die Indizes ausgegeben bekommen. Für Matrizen sind diese weniger leicht zu nutzen, weil die Nummerierung fortlaufend spaltenweise vorliegt. In unserem Fall einer 5 x 5 Matrix heißt das z.B., dass das Element in der 1. Zeile der 3. Spalte (also der eine fehlende Wert) den Index 11 trägt.
Bei Vektoren kann man arr.ind = TRUE weglassen, da diese entweder nur aus einer Spalte oder einer Zeile bestehen.
which(is.na(daten), arr.ind = TRUE) row col
Vpn_1 1 1
Vpn_1 1 3
Vpn_4 4 3
Vpn_4 4 519.3 Wie kann man die Missings zählen (und verorten)?
Die genaue Anzahl der Missings zu kennen ist wichtig, um ein Gefühl dafür zu kriegen, wie vollständig ein Datensatz ist. Dazu kombinieren wir die is.na()-Funktion mit anderen Funktionen, die FALSE (d.h. vorhandenen Werte) und TRUE (d.h. fehlenden Werte) zählen.
19.3.1 Alle Missings eines Datensatzes
Zuerst schauen wir uns die Gesamtanzahl der Missings aller Elemente im Datensatz an.
table(is.na(daten))
FALSE TRUE
21 4 19.3.2 Missings in einzelnen Spalten oder Zeilen
Spaltenweises Zählen der Missings gibt Informationen über mögliche Probleme mit bestimmten Variablen. Zeilenweises Zählen der Missings gibt beispielsweise Informationen über Teilnehmende, die die Fragen nicht vollständig beantwortet haben.
Es ist daher wichtig, sich einen Überblick darüber zu machen, ob sich bei bestimmten Variablen oder bei bestimmten Personen besonders viele Missings häufen. Wenn das der Fall sein sollte, muss man überlegen, wie man damit umgeht (dazu mehr im späteren Verlauf).
Wenn wir eine bestimmte Spalte oder Zeile betrachten möchten, können wir die is.na()-Funktion mit der table()-Funktion kombinieren. Zweiteres sorgt dafür, dass wir eine Häufigkeitstabelle von TRUE und FALSE ausgegeben bekommen.
Wir können auf verschiedenem Wege auf eine Spalte bzw. Zeile eines Datensatzes referenzieren.
table(is.na(daten$Var_1)) # Datensatz$Spaltenname
FALSE TRUE
4 1 table(is.na(daten["Var_1"])) # Datensatz["Spaltenname"]
FALSE TRUE
4 1 table(is.na(daten["Vpn_1",])) # Datensatz["Zeilenname"]
FALSE TRUE
3 2 table(is.na(daten[,1])) # Datensatz[,Spaltenindex]
FALSE TRUE
4 1 table(is.na(daten[1,])) # Datensatz[,Zeilenindex]
FALSE TRUE
3 2 Achtung: Die ersten drei vorgestellten Möglichkeiten,
$undDatensatz["Spalten- bzw. Zeilenname"], funktionieren nur bei Dataframes, und nicht bei Matrizen. Die Möglichkeit der Indexierung können wir auch bei Matrizen nutzen.
19.3.3 Missings in allen Spalten oder Zeilen
Wenn man sich einen Überblick über die Missings in allen Variablen bzw. bei allen Personen verschaffen möchte, kann man dafür colSums() bzw. rowSums() mit dem is.na()-Befehl kombinieren. Damit werden spalten- bzw. zeilenweise Summen von TRUE (d.h. den Missings) gebildet.
Um die Größenordnung der Missings besser beurteilen zu können, sollte man sich der maximal möglichen Anzahl der Elemente in einer Spalte bzw. Zeile bewusst sein. Diese können wir mit nrow() bzw. ncol() in Erfahrung bringen.
# Übersicht der Missings in allen Variablen (Spalten)
colSums(is.na(daten))Var_1 Var_2 Var_3 Var_4 Var_5
1 0 2 0 1 # ... im Vergleich zur maximalen Anzahl an Beantwortungen
nrow(daten)[1] 5# Übersicht der Missings in allen Personen (Zeilen)
rowSums(is.na(daten))Vpn_1 Vpn_2 Vpn_3 Vpn_4 Vpn_5
2 0 0 2 0 # ... im Vergleich zur maximalen Anzahl der beantwortbaren Fragen
ncol(daten)[1] 519.3.3.1 Visualisierung der Missings
Mit der Funktion aggr() aus dem Paket VIM kann man sich zwei Plots ausgeben lassen, die den relativen Anteil von Missings in den einzelnen Variablen und die Anzahl an Missings in bestimmten Kombinationen von Variablen (d.h. in den Zeilen) ausgeben.
Wenn man summary(aggr()) nutzt, bekommt man sowohl die grafische Visualisierung als auch eine Übersicht der Häufigkeiten.
# install.packages("VIM")
library(VIM)
summary(aggr(daten))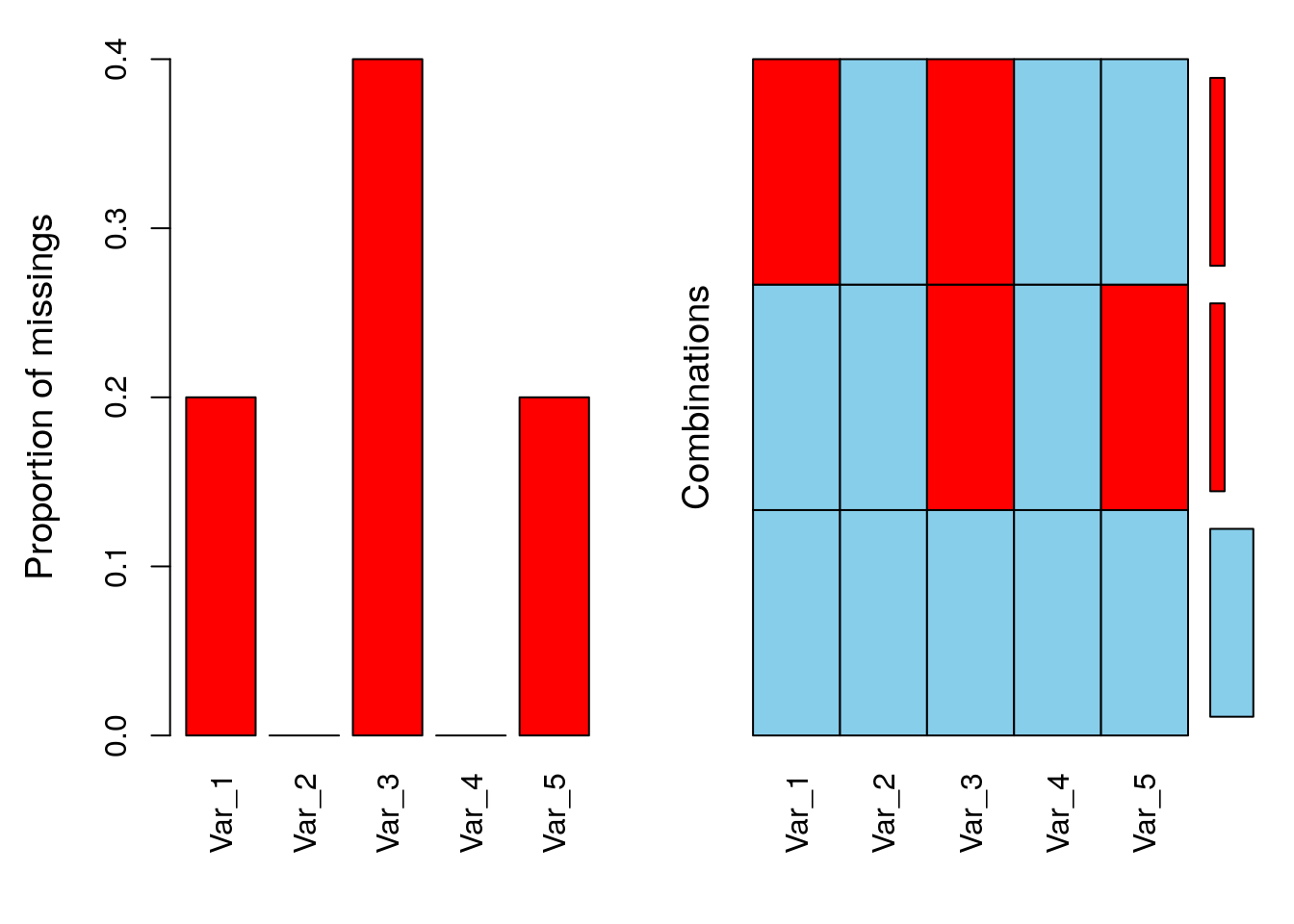
Missings per variable:
Variable Count
Var_1 1
Var_2 0
Var_3 2
Var_4 0
Var_5 1
Missings in combinations of variables:
Combinations Count Percent
0:0:0:0:0 3 60
0:0:1:0:1 1 20
1:0:1:0:0 1 20Im linken Plot sehen wir, dass nur Missings in Var_1, Var_3 und Var_5 vorhanden sind. Außerdem sehen wir auf der \(y\)-Achse den relativen Anteil an Fällen in den Variablen. In der Übersicht unter der Tabelle sehen wir die absoluten Häufigkeiten für alle Variablen (Missings per variable). Im rechten Plot sehen wir die vorhanden Kombinationen von Missings in den Variablen. Blau zeigt an, dass kein Missing vorhanden ist; rot zeigt an, dass ein Missing vorhanden ist. Beispielsweise zeigt die unterste Reihe (die komplett blau ist) eine Kombination, in der keine Missings in Variablen vorhanden sind. Rechts daneben sieht man einen Balken, der den Anteil dieser Kombination im Verhältnis zu den anderen Kombinationen darstellt. Der Balken in der untersten Reihe ist der größte, d.h. dass diese Kombination am häufigsten vorkommt und somit die meisten Fälle (Zeilen) im Datensatz keine Missings enthalten. Leider bekommen wir hier keine Häufigkeiten dafür angezeigt. Dazu können wir aber in die unten stehende Übersicht schauen. (Missings in combinations of variables), in der wir absolute und relative Häufigkeiten ausgegeben bekommen.
19.4 Literaturempfehlungen
Für ein tiefergehenden Einblick empfehlen wir Euch die folgenden Arbeiten:
Allison, P. D. (2002). Missing Data. In P. D. Allison (Ed.), The Sage Handbook of Quantitative Methods in Psychology (pp.72-89). Thousand Oaks, CA: Sage Publications Ltd. Abgerufen über http://www.statisticalhorizons.com/wp-content/uploads/2012/01/Milsap-Allison.pdf
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Missing Data. In J. Cohen, P. Cohen, S. G. West, & L. S. Aiken (Eds.), Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences (pp. 431-451)*. Hillsdale, NJ: Erlbaum.
(für HU-Studierende über ub.hu-berlin.de zugänglich)
Little, R. J. A. (1988). A test of missing completely at random for multivariate data with missing values. Journal of the American Statistical Association, 83(404), 1198–1202.
(für HU-Studierende über ub.hu-berlin.de zugänglich)
Schafer, J. L., & Graham, J. W. (2002). Missing Data: Our View of the State of the Art. Psychological Methods, 7(2), 147-177. https://psycnet.apa.org/doi/10.1037/1082-989X.7.2.147
Um eine möglichst exakte Replikation der Funktionen zu gewährleisten gibt es im folgenden relevante Angaben zum System (R-Version, Betriebssystem, geladene Pakete mit Angaben zur Version), mit welchem diese Seite erstellt wurde.
sessionInfo()R version 4.4.2 (2024-10-31)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.1 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so; LAPACK version 3.12.0
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
time zone: Etc/UTC
tzcode source: system (glibc)
attached base packages:
[1] grid stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] VIM_6.2.2 colorspace_2.1-1
loaded via a namespace (and not attached):
[1] cli_3.6.3 knitr_1.49 rlang_1.1.4
[4] xfun_0.49 Formula_1.2-5 DEoptimR_1.1-3
[7] car_3.1-3 jsonlite_1.8.9 data.table_1.16.2
[10] zoo_1.8-12 ranger_0.17.0 htmltools_0.5.8.1
[13] e1071_1.7-16 nnet_7.3-19 lmtest_0.9-40
[16] sp_2.1-4 rmarkdown_2.29 abind_1.4-8
[19] evaluate_1.0.1 carData_3.0-5 MASS_7.3-61
[22] fastmap_1.2.0 yaml_2.3.10 compiler_4.4.2
[25] robustbase_0.99-4-1 htmlwidgets_1.6.4 Rcpp_1.0.13-1
[28] vcd_1.4-13 lattice_0.22-6 digest_0.6.37
[31] laeken_0.5.3 class_7.3-22 Matrix_1.7-1
[34] tools_4.4.2 proxy_0.4-27 boot_1.3-31 Für Informationen zur Interpretation dieses Outputs schaut auch den Abschnitt Replizierbarkeit von Analysen des Kapitels zu Paketen an.